

(The black areas have data costs = 0 for all labels.)
Image size: 256 x 256, labels: 256 Data term: squared differences, except in hole where data costs = 0 for all labels Smoothness term: squared differences (L2 norm), lambda=5
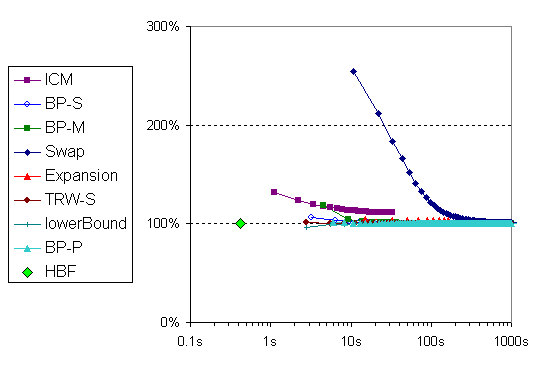
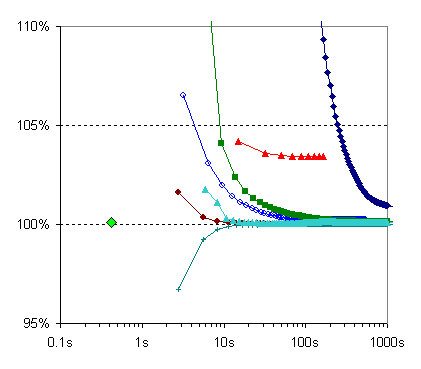
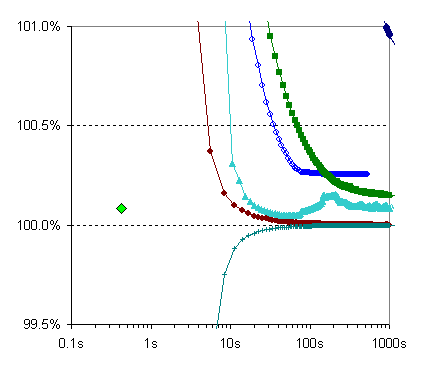
BP-P: Pedro Felzenszwalb's BP implementation [P. Felzenszwalb and D. Huttenlocher, Efficient belief propagation for early vision, IJCV 70(1), 2006].
HBF: Rick Szeliski's fast quadratic solver using hierarchical basis functions [R. Szeliski, Locally adapted hierarchical basis preconditioning, SIGGRPAH 2006].
Since this is a quadratic problem, there is a single (real-valued) global minimum, which can be found with a quadratic solver. If ICM was run with real-valued variables, it would converge to this solution. For comparison, the plots contain the solution obtained after 5 iterations of the (HBF) solver, which takes less than 0.5 seconds. The solution, when rounded to the nearest integers, has an energy about 0.1% higher than the best integer solution found by TRW-S.
Input image (noise contaminated), and the original image ("ground truth"):


(The black areas have data costs = 0 for all labels.)
All algorithms use the input intensities as start values.
Result images and their energies:
 |